For those of you who were confused even after reading the comments: (a)(b) basically means a*b. My mind just didn’t connect that to the fact that (x-x)=0. in the (a-x)(b-x) stuff is also (x-x) which = 0, and anything * 0 = 0, so no matter the value of literally everything else in the equation, it all equals out to 0 because every single () will get multiplied by (x-x), which is 0. There, hopefully that will clear it up for anyone remaining lost. And like all good jokes, they are always best when you have to explain them.
Even if the x-x term didn’t exist, the equation is already simplified (fully factored) so there is nothing to do anyway.
is already simplified (fully factored)
No it isn’t, given one of the factors is equal to zero. That’s like saying 2/4 is fully simplified when clearly it isn’t. Students lose marks in tests for not simplifying their answers. Writing 2/4 as an answer would only get half-marks. Similarly, the only full-marks answer to this question is 0.
My stipulation was that the x-x term didn’t exist, such that the equation would be fully simplified (assuming the request was “factor and simplify”). Yes, you could also “expand and simplify” (as in your other comment) but I would argue the result of that would be less simplified than the factored version. Eye of the beholder type thing.
I agree that if x-x did exist as a term then expand and simplify would be correct (that is if x-x wasn’t noticed to be 0 immediately and no expansion would be needed at all).
My stipulation was that the x-x term didn’t exist, such that the equation would be fully simplified
And it STILL wouldn’t be simplified.
“factor and simplify”
Factorising is the opposite process to expanding, so no, there’s no such thing as “factor and simplify”.
I would argue the result of that would be less simplified than the factored version. Eye of the beholder type thing.
It’s a definition of Maths thing. Simplified answers don’t have brackets in them.
Are you a high school math teacher by chance? Because you’re using a rigid definition of simplify that I don’t necessarily agree with. For example, if I give you the fraction:
(x2+(a+b)x+ab)/(x2+ax-bx-ab)
And told you to simplify, what would you do?
Are you a high school math teacher by chance?
Yep.
Because you’re using a rigid definition of simplify that I don’t necessarily agree with.
You don’t agree with Maths textbooks? 😂
“And told you to simplify, what would you do?” - I would ask you what on Earth it’s supposed to say, given it’s formatted all weird! 😂
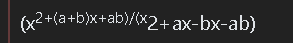
It’s raw text on my side, looks fine. It might be fixed now? Not sure how the formatting works for equations on Lemmy.
And correct, I don’t agree with whatever you are interpreting from your math textbooks because “simplify” literally means to make the equation easier to understand. You are arguing that “expand and simplify” is the exact same thing as “simplify”… Which if they were, it would just be in word, wouldn’t it… Sometimes factoring is prudent. Other times expansion is necessary. This is exemplified by the math I gave in the previous comment.
And thanks for the downvotes. I hope you don’t treat your students the same way when they question your ultimate wisdom by dismissing them outright. I certainly don’t to mine.
“simplify” literally means to make the equation easier to understand
Nope. It means to present it in the simplest way possible. e.g. 5/10=1/2.
You are arguing that “expand and simplify” is the exact same thing as “simplify”
No I’m not. I’m saying “expand and simplify” is a thing in all high school Maths textbooks, “factor and simplify” isn’t a thing in any of them.
“Sometimes factoring is prudent” - if you’re trying to solve an equation, yes, but solving and simplifying aren’t the same thing. If I arrive at an answer of 5/10 then I have solved but not simplified. Sometimes it’s not even possible to simplify, because the answer is already in the simplest form possible, such as an answer of 1/2. I teach students when to recognise when something can be simplified and when it can’t. Your original contention was that the Term was already simplified, and it wasn’t.
“And thanks for the downvotes.” - I downvote anything that is incorrect, just like a student would lose marks for same.
What’s the right term then? “Multiplied through?” ? “Complicated?”
Expand
Expand
As in “expand and simplify”. If you only expanded then you haven’t simplified yet.
Or “factor and simplify”.
Or “factor and simplify”
Factorising is the opposite process to expanding, so no, that isn’t simplifying.
My point (made poorly) was there is “expand and simplify” and also “factor and simplify”. Two different things.
My point (made poorly) was there is “expand and simplify” and also “factor and simplify”. Two different things.
And my point is there’s no such thing as “factor and simplify”, since they are opposite operations to each other.
Fun fact, omitting the (x-x) zero term and expanding the entire polynomial, you’d get something with 2^25 = 33,554,432 terms. May be slightly excessive!
Couldn’t you combine a lot of like terms as you went along, though? A polynomial of the order x26 would only have 27 terms.
No, because each coefficient is its own variable; they’re not constants.
because each coefficient
There’s only 1 coefficient - in this case it’s (a-x) - the rest are just factors.
they’re not constants
They could be - we haven’t been given that information.
Huh, I’m so used to polynomials being in the form ax^2 + bx + c that I never considered that every letter might be a variable.
33,554,432 terms
Actually it would be that many factors. The whole thing is a single Term.
For those that struggled like me…
Going from a-z, write out the last three multiplicands.
X-X
Ah
For those of you who still struggled like me, a multiplicand in this case refers to one of the (n-x) terms.
a multiplicand in this case refers to one of the (n-x) terms
Well, that’s what was apparently meant, but in fact the correct terminology here is factors. There’s only multiplicands (and multipliers) with an explicit multiplication sign. axb - multiplicand a and multiplier b, ab - Term with factors a and b, and a is the coefficient of this Term.
deleted by creator
This was impossible to answer prior to 3 BC.
Unless you were Mayan. They had a concept of zero, or so I heard. But they lacked the letters, a-z and the parentheses :p
Why?
0 wasn’t invented yet.
Mesopotamians invented it because year 0 was approaching, so there was a dire need to represent such number.
TIL they had ghost concerts back then
0 BCE kind of sucked. Thankfully, they figured it out and 0 CE was awesome.
That’s when the number 0 was introduced in India.
Ah, I forgot zero was so recent.
Solution?
0
There’s an (x - x) in there
Technically there is a (x - 𝑥) in there.
U+1D465 != xso this post is a little mehMathematicians do weird stuff to get more letters, but I’ve never seen anyone use x and 𝑥 for different things
I’ve never seen anyone use x and 𝑥 for different things
Yeah, me neither. I have had situations where I needed to distinguish between u, v, nu, and upsilon though. I had to be very careful with my handwriting that day…
They also wouldn’t want to be ambiguous. If I was trying to write this problem the a, b, c… would get replaced by something like a_1, a_2,…, a_26 to be clearer. This problem works as a fun gotcha but isn’t something that would come up in the real world.
the first variables aren’t roman. they’re italicized as well. idk where you’re getting the x vs x thing.
Assuming both x represent the same number. There’s no reason to assume the ellipses should include x-x. Why would alphabetic order be involved at all?
have you never taken math? I’m seriously asking because you’re incredibly wrong in both statements.
duh…
Do do, do do do do do…
Zero
0






